No other tool has been as influential as Desmos in helping my students do mathematics.
The recent announcement to include access to the Desmos online graphing calculator on the Standards of Learning tests is a huge win for both math teachers and students. If Desmos is the best tool for students to use to learn and understand mathematical topics, then they should have access to the same tool for all assessments.
Every school year, I set out with the goal of creating more opportunities for my students to actively do mathematics. That means students spend less time listening to me tell them what they need to know and more time observing, discovering, and connecting mathematical ideas. It means students spend less time memorizing procedures and more time understanding concepts. That deeper understanding leads to procedural fluency. Both the Desmos graphing calculator and the activity builder assist me in creating these opportunities for my students, and it all helps them learn and enjoy math.
The Graphing Calculator
The Desmos graphing calculator provides a free and intuitive alternative to other graphing calculators. The free calculator can be accessed on any device through a browser or by downloading the app. Once the app is downloaded or the calculator is loaded into the browser, an Internet connection is not needed to use the calculator. My students have access to the calculator at home and quickly learn how to use the calculator with little instruction. There are very few menus to navigate or button pushing sequences to remember.
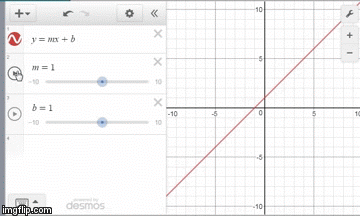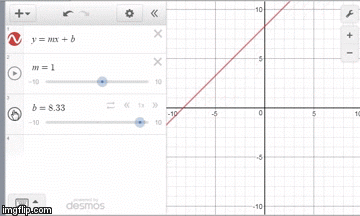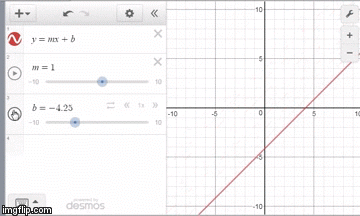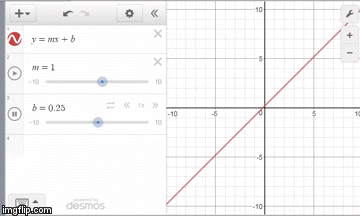
In addition to being easier to use, the Desmos graphing calculator makes learning mathematics more visual with its clean interface. Users can always see the expression list and graph side by side. The graph also updates on every keystroke, helping students make connections across multiple representations. One of the most powerful features in the graphing calculator, sliders, makes a graph dynamic and gives students the chance to observe and generalize different parameters in a particular equation. In the example below, instead of the teacher telling students what b represents in the equation y = mx + b, students can observe and hypothesize on their own.
Teachers can then facilitate a classroom conversation where students work collaboratively to generalize important information. This use of sliders and student led discussion works well for equations and functions across all mathematics courses.
Finally, the graphing calculator also helps students see the beauty of math and inspires creativity. At the end of the year, my students use the graphing calculator or the geometry tools to create an original art project. The amount of time and effort students are both willing and excited to put into this project demonstrates the allure of the tools.
Activity Builder
The Desmos Activity Builder allows teachers to utilize all the features of the graphing calculator to create activities that promote student discovery and discourse. You can begin creating your own lessons with this template. These activities help change the way teachers instruct and students learn. Desmos activities are designed to promote mathematical conversations and make learning social.
One example of an activity that promotes mathematical conversations is the Polygraph game. Modeled after the board game Guess Who, students ask questions and guess which object their classmate picked. Polygraph activities are a great way to both introduce and practice vocabulary. Instead of having students copy and memorize definitions, I begin teaching vocabulary by having students play Polygraph to see what features they notice and identify the language students use to describe those features. The teacher dashboard allows me to keep track of all the games and student responses in real time. After a few rounds, I pause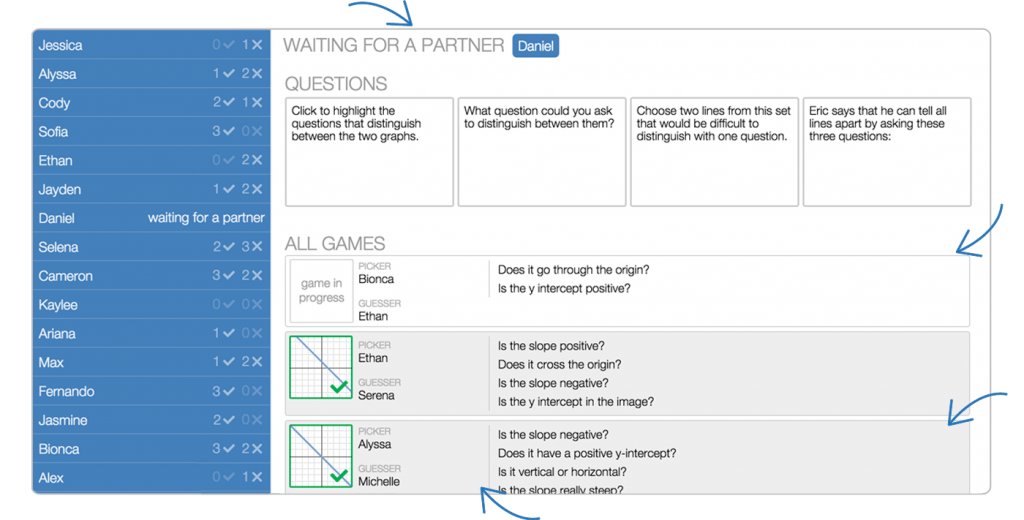 
the class and help students develop their informal language into formal vocabulary. Students then have an opportunity to practice the new vocabulary by playing a few more rounds. The Polygraph game creates a need for common language to help students describe the objects more effectively and efficiently.
Creating a need for new tools and promoting collaboration are common themes throughout all the Desmos activities. Challenge Creator occurs at the end of several activities and allows students to create challenges for each other and ask each other questions. Students become more invested and engaged as they create and share those creations with classmates. Marbleslides is a game that forces students to use their understanding about equations and graphs to collect stars. The game provides feedback that helps students see what their answers mean and then gives them the opportunity to improve their thinking and revise their work.
Desmos faculty member Christopher Danielson (From Counting to Calculus: What Stays the Same?) believes doing mathematics means, “working with unfamiliar objects, expressing ideas for which you don’t have words, building arguments, inventing strategies, extending ideas, and playing.”
I want my students to have as many opportunities as possible to think and learn in these ways instead of merely receiving and memorizing information. The Desmos Activity Builder has been the single most influential tool in helping me create more opportunities for students to think mathematically and do mathematics. The Desmos Guide to Building Great (Digital) Math Activities describes the pedagogy Desmos values and further emphasizes the impact Desmos tools can have on classroom teaching and learning. The guide has helped me with running and creating Desmos activities and in planning low-tech lessons as well. This pedagogical shift has helped my students develop a deeper conceptual understanding of mathematics before gaining procedural fluency.
Authorship Information:
Nolan Doyle is a mathematics teacher at Clover Hill High School. He is also a Desmos Teaching Fellow and Desmos Certified Presenter. He has taught for 10 years with the last 6 years being in Chesterfield County. He enjoys spending time with his wife and two kids, the outdoors, UVA basketball, and playing soccer.